精通BM25：深入探讨算法及其在Milvus中的应用

搜索引擎中的信息检索算法对于确保搜索结果与用户查询的相关性至关重要。

想象一个用例，我们正在寻找关于特定主题的研究论文。当我们在搜索引擎中输入“RAG”作为关键词时，我们显然希望得到一系列讨论不同RAG方法的论文，而不是其他一般的NLP方法。这就是信息检索算法发挥作用的地方。它们确保我们得到的论文与我们的关键词高度相关。

信息检索中有两种常用的算法：TF-IDF和BM25。在本文中，我们将讨论关于BM25的所有内容。然而，在我们深入讨论之前，最好我们先理解TF-IDF的基础知识，因为BM25基本上是TF-IDF的扩展。

TF-IDF的基本原理

术语频率-逆文档频率（TF-IDF）是一种基于统计方法的信息检索算法。它衡量一个关键词在文档中相对于一组文档的重要性。

从它的名字可以看出，TF-IDF由两个组成部分构成：术语频率（TF）和逆文档频率（IDF）。它们衡量不同的方面，但最终，我们将两个组成部分相乘，以获得估计单词在文档中相关性的最终得分。

传统TF-IDF的TF部分衡量特定关键词在文档中的出现次数。

12.1.PNG

上面的等式相当直观：我们在文档中找到的关键词实例越多，TF值就会越高。 另一方面，IDF部分衡量包含我们关键词的文档集合中文档的比例。换句话说，这部分告诉我们的关键词出现在多少文档中。

12.2.PNG

我们可以看到，我们的关键词在文档中出现的频率越高，其IDF得分就越低。这是因为我们想要惩罚常见的单词，如“a”、“an”、“is”等，因为它们往往出现在许多文档中。

在计算TF和IDF组成部分之后，我们将结果相乘，以获得关键词的最终TF-IDF得分。

12.3.PNG

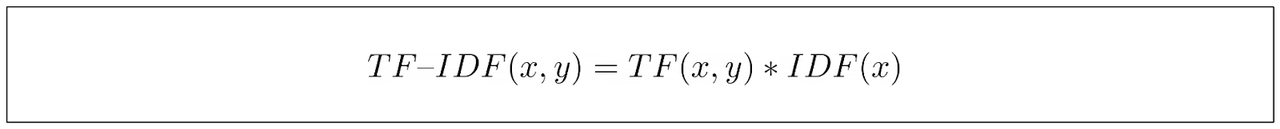
从上面的最终等式中，我们可以看到TF-IDF通过给它分配更高的分数来捕捉关键词的重要性，如果它在一个文档中频繁出现，但在其他文档中很少出现。

当给定用户关键词或查询时，搜索引擎可以使用TF-IDF分数来衡量关键词与文档集合之间的相关性。然后，搜索引擎可以对文档进行排名，并向用户展示最相关的文档。

TF-IDF的问题

TF-IDF公式有两个可以改进的问题。

首先，假设我们有“兔子”这个词作为查询，并且有两个文档进行比较。在文档A中，“兔子”出现了十次，而该文档有1000个单词。另一方面，我们的关键词在文档B中只出现了一次，而该文档有十个单词。

仔细观察，我们可以立即看到TF-IDF的局限性。文档A的TF分数将是10，而文档B的分数将是1。因此，与文档B相比，会向我们推荐文档A。

12.4.PNG

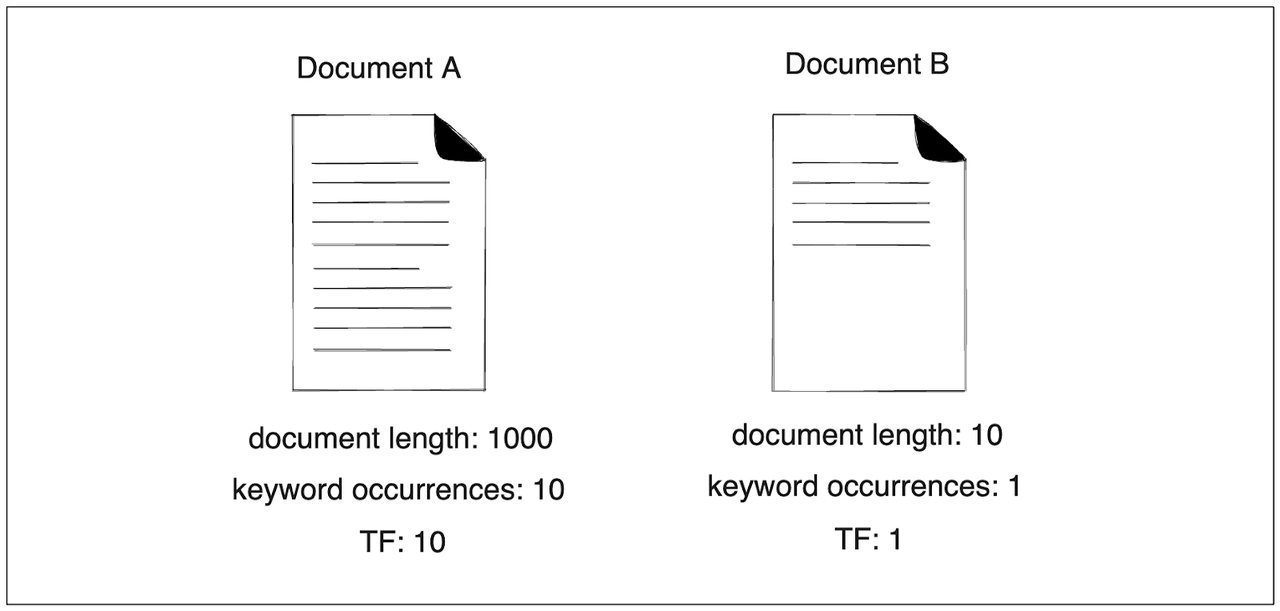
然而，如果我们考虑文档长度，我们可能会认为我们更喜欢文档B而不是文档A。

当一个文档非常短并且包含“兔子”一次时，这是一个更有说服力的迹象，表明该文档真正讨论了兔子。相反，如果一个文档有成千上万个单词，并且它提到了“兔子”十次，我们不能肯定该文档专门讨论兔子。

为了解决这个问题，TF-IDF的归一化变体将TF除以文档长度。然后，TF部分的TF等式如下所示： 12.5.PNG

但它仍然有一个需要优化的问题，这与关键词饱和有关。

如果我们看一下TF-IDF的TF部分，我们可以发现我们的关键词在文档中出现的次数越多，TF就会越高。这种关系是线性的，这似乎是一件好事，因为我们想要不断地奖励包含我们关键词的文档。然而，如果我们在一个文档中找到了“兔子”400次，这真的意味着这个文档是另一个只包含200次出现的文档的两倍相关吗？

我们可以认为，如果关键词“兔子”在文档中出现这么多次，我们可以说这个文档肯定与我们的关键词相关。这个文档中关键词的额外出现不应该以线性比例增加其相关性的可能性。

文档中关键词出现次数从2到4的得分跳跃应该比从200到400的跳跃有更大的影响。而这正是目前TF-IDF公式所缺少的。

12.6.PNG

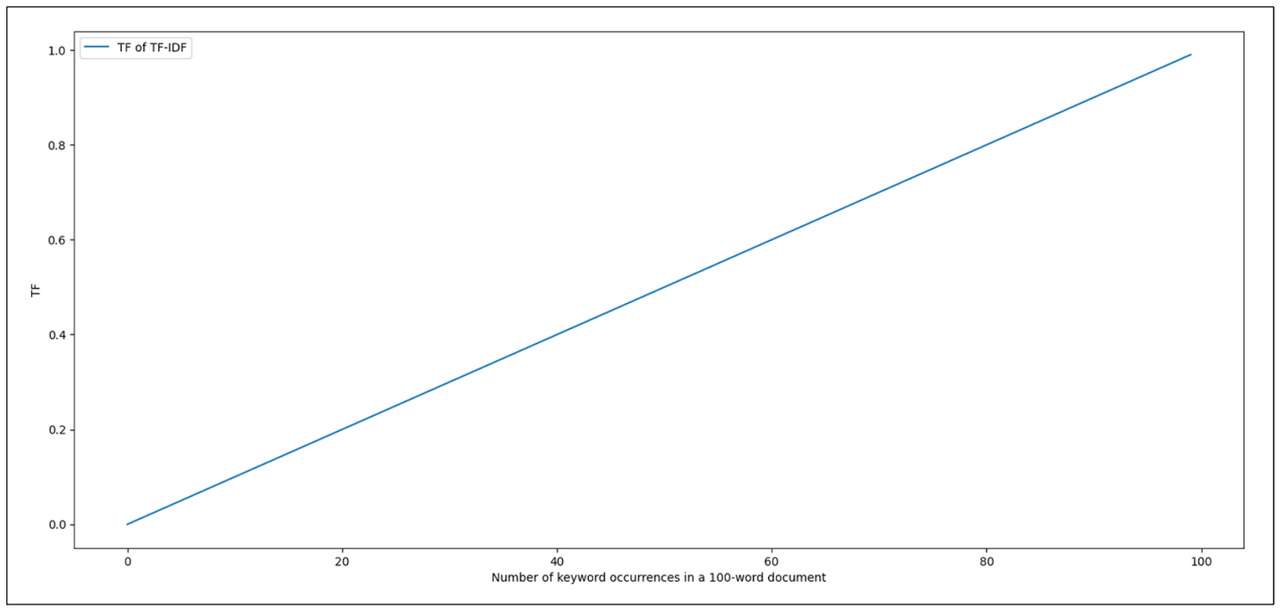
如您从上面的可视化中看到的，假设我们将文档中的单词数固定为100，随着我们关键词的出现次数增加，TF-IDF的TF分数线性增加。

那么，我们如何改进TF-IDF呢？这就是我们需要BM25算法的地方。

BM25的基本原理

最佳匹配25（BM25）是一种算法，可以看作是对传统TF-IDF的改进，通过解决前一节中提到的所有问题。

让我们首先讨论关键词饱和。TF-IDF的TF部分将随着关键词在文档中的出现次数线性增长。从2到4个关键词的得分跳跃将与从50到52个关键词的跳跃相同。

BM25引入了一个与TF-IDF略有不同的TF部分公式，我们将逐步揭示每个组成部分，以使我们更容易理解其背后的原理。

首先，BM25在其TF等式中引入了一个新参数，而不是仅仅依赖于关键词的出现次数： extra.png

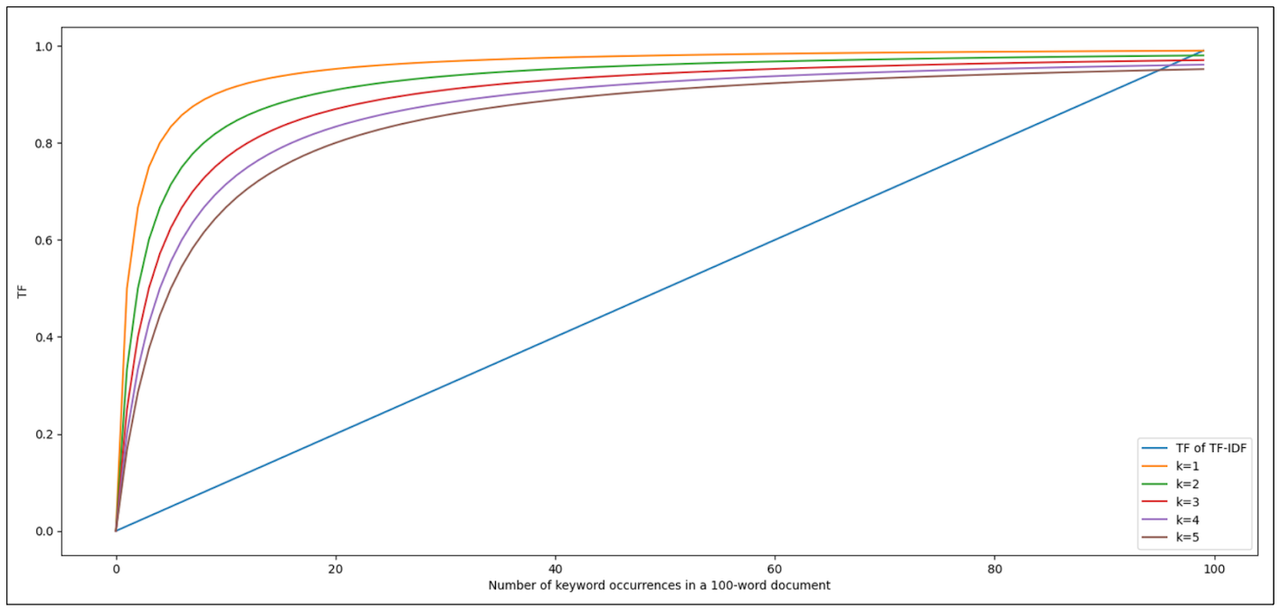
上面的参数k作为控制我们关键词的每次增量出现对TF分数的贡献的参数。让我们看一下下面的可视化，看看k的影响 12.8.png

正如您所见，前几次关键词出现对整体TF分数的影响很大。然而，随着我们的关键词在文档中出现得越来越多，它对整体TF分数的贡献就变得越来越不相关。k值越高，每次出现我们关键词对TF分数的贡献增长就越慢。这解决了与TF-IDF相关的关键词饱和的缺点。

与传统TF-IDF相比，BM25的另一个基本改进是BM25考虑了文档长度。使用BM25，一个包含一个关键词的10个单词的文档将比包含10个关键词的1000个单词的文档更强。

12.9.png

术语∣D∣代表文档长度，而avg(D)代表我们语料库中文档的平均长度。您已经可以看到这种文档归一化对我们k参数的影响。如果文档比平均长度短，TF/(TF+k)的值将增加，反之亦然。换句话说，较短的文档将比较长的文档更快地接近饱和点。

然而，我们不能以同样的方式对待所有语料库。在某些语料库中，文档的长度非常重要，而在其他语料库中，文档的长度根本不重要。因此，在TF等式中引入了一个额外的参数b来控制文档长度在整体分数中的重要性。 我们可以看到，如果我们将b的值设置为0，那么比率D/avgD将根本不会被考虑，这意味着我们不重视文档的长度。同时，值1表示我们非常重视文档的长度。

12.10.png

上面的等式是BM25中使用的TF部分的最终等式。但是IDF部分呢？

BM25的IDF部分与TF-IDF的等式略有不同。BM25的IDF等式可以定义如下： 其中N是语料库中文档的总数，DF是包含我们关键词的文档数量。上面的等式源于研究人员进行的经验观察，他们希望推导出一个能够捕捉排名函数行为的等式，而不仅仅是尝试不同的值并希望得到最好的结果。

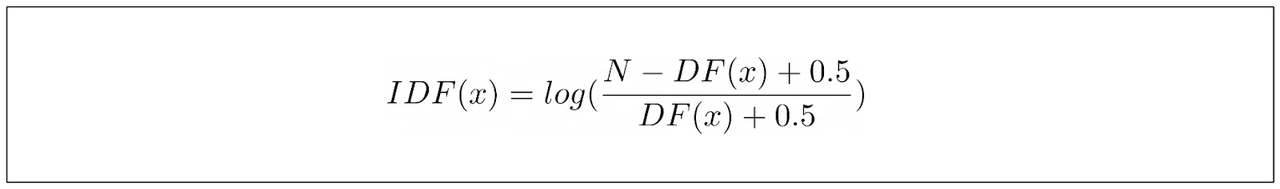12.11.png

然而，这个IDF等式有一个主要问题：如果我们的关键词出现在超过一半的语料库中，它将导致负值。这在信息检索用例中没有意义。在信息检索中，分数不能低于我们的关键词在我们的语料库中的任何文档中都找不到的情况。

为了缓解这个问题，通常在IDF等式中添加一个标量值1，使其与TF-IDF的IDF项相同。

我们有了，下面是BM25计算文档中特定关键词得分的最终等式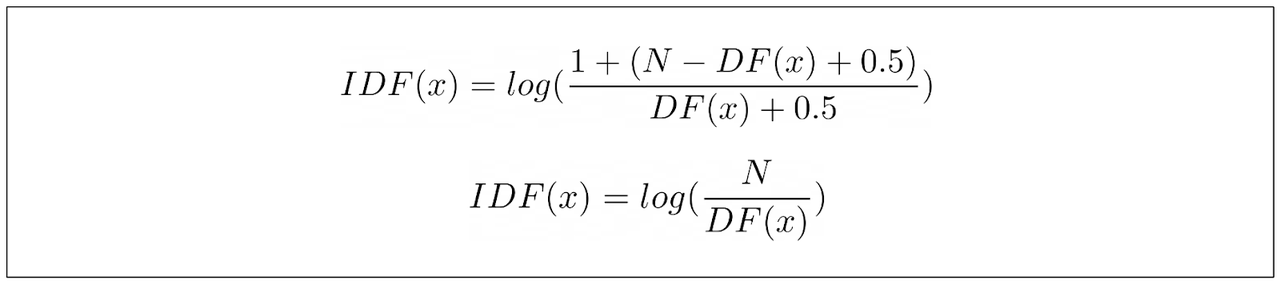： 12.13.png

顺便说一句：我们并没有真正讨论上面TF部分分子中的项(k+1)。然而，由于这个项不影响整体BM25结果的关系，你可以忽略这个项。

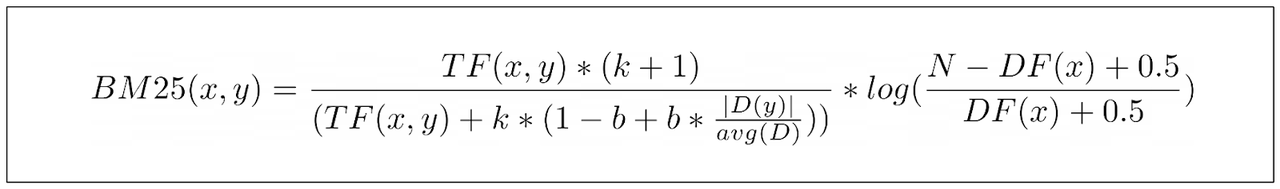12.14.png

BM25的参数

在前一节中，我们了解到BM25有两个我们可以根据自己的用例调整的参数：一个叫做k，另一个叫做b。现在，问题是，我们应该为这两个参数设置什么值呢？

在现实世界的应用中，k=1.2和b=0.75的值在大多数语料库中都工作得很好。然而，你可以实验这两个参数的值，以找到最适合你用例的值。这是因为选择k和b的值遵循“没有免费的午餐”理论，意味着没有适用于所有用例的通用“最佳”k和b值。

根据实验，k的值往往在0.5到2的范围内是最优的，而b的值往往在0.3到0.9的范围内是最优的。

在调整k的值时，问问自己这个问题：我的文档的平均长度是多少？

如果你有一系列非常长的文档，那么一个关键词很可能会出现几次，即使文档实际上并没有讨论那个关键词。在这种情况下，你可能想要将k值设置在一个更高的范围内，以便TF分数的饱和点不会太快达到。相反的情况也是如此。如果你的文档平均长度很短，那么你可能会想要将k值设置在一个较低的范围内。

关于b值，问问自己这个问题：我有哪些类型的文档，在我的用例中，文档的长度会影响关键词的相关性吗？

例如，如果你有一系列长篇科学文档，很可能这些文档中包含的大多数单词都是重要的。因此，你可能想要将b设置在一个较低的范围内。同时，如果你有一系列观点性和主观性的文档，你可能想要将b值设置在一个较高的范围内，以惩罚在短文档和长文档中可能出现的关键词垃圾邮件。

TF-IDF与BM25的比较

BM25确实是对传统TF-IDF方法的改进。然而，这并不意味着我们应该总是使用BM25而不是TF-IDF。在某些用例中，使用TF-IDF可能就足够了，因为它比BM25更简单，计算成本也更低。

以下是TF-IDF和BM25在相关性评分（TF-IDF和BM25的最终结果）、精确度、处理较长文档的能力以及最佳使用场景方面的比较分析列表。

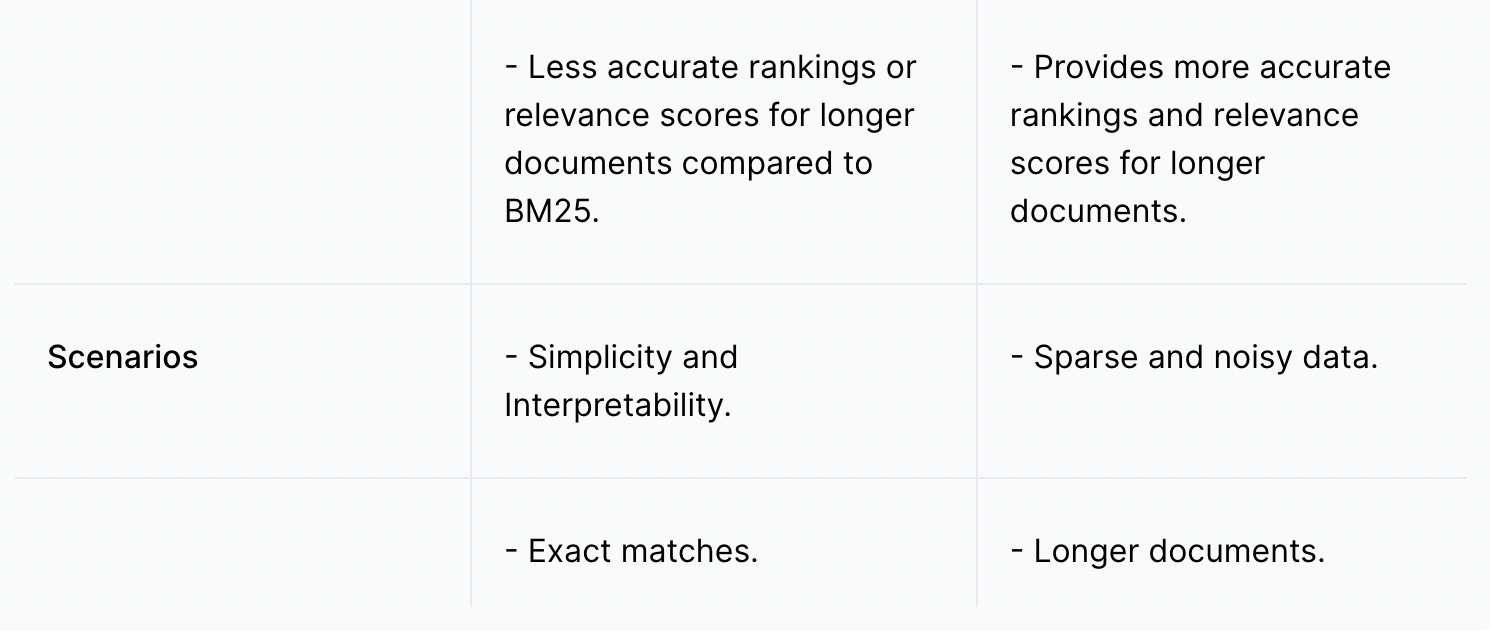12.表3.png 12.表2.png 12.表1.png

在Milvus中实现BM25

在本节中，我们将实现BM25进行语义搜索，并将整个过程与Milvus集成。如果你想跟随操作，可以查看这个笔记本。 在我们深入Milvus集成BM25之前，请确保安装了Milvus独立版和SDK。你可以在我们的Milvus文档页面上找到完整的安装指南。 让我们首先加载所有必要的库。

from pymilvus.model.sparse import BM25EmbeddingFunction

作为数据，我们将使用一个你可以在Kaggle上免费下载的电子商务数据集。让我们加载数据集，并使用Milvus实例化BM25模型。

df.columns

code block

如你所见，我们的数据集中有多个列。为了向量搜索演示的目的，我们将只使用标题列作为我们的语料库。 BM25EmbeddingFunction类是Milvus实现的BM25嵌入模型，它将文档或查询转换为其稀疏嵌入表示。但在我们能够将任何文档和查询转换为稀疏嵌入之前，我们需要在我们的语料库上拟合BM25模型，以收集每个令牌的统计信息。

analyzer = build_default_analyzer(language="en")

根据产品标题创建语料库

code block

使用分析器实例化BM25EmbeddingFunction

python bm25_ef = BM25EmbeddingFunction(analyzer) 在语料库上拟合模型以获取语料库的统计信息 bm25_ef.fit(corpus) 上面的build_default_analyzer函数是Milvus的一个内置函数，它执行多个功能。首先，它删除特定语言中的常见停用词，对每个剩余的单词进行分词，然后收集每个令牌的相关性统计信息。 现在假设我们有5个产品标题。我们可以使用encode_documents方法将每个产品标题转换为其稀疏向量表示。

'Cloudz"The Big Bag" Travel & Sport Duffle Bag']

为产品标题创建嵌入

Sparse dim: 673273 (1, 673273)

每个文档的向量维度对应于我们在build_default_analyzer函数内经过停用词过滤过程后的语料库中可用的总令牌数。每个向量元素代表文档中每个令牌的相关性得分。 让我们将所有这些向量嵌入插入Milvus向量数据库中。首先，我们将定义表的模式。然后，我们选择适当的索引和相似性度量，以便在执行向量搜索时使用。 由于BM25产生稀疏向量，那么我们可以使用倒排索引或弱与（WAND）算法等索引方法。然而，由于我们的稀疏向量具有高维性，我们可以使用倒排索引。这种方法将每个维度映射到我们嵌入中的非零值，提供在搜索过程中直接访问相关数据的途径。 作为向量搜索的度量，Milvus目前只支持内积，所以我们将使用它。

col.create_index("product_title_vector", sparse_index)

将数据插入模式

col.flush()

现在我们准备执行向量搜索。假设我们有一个查询：“我应该为旅行买什么产品？”。然后我们可以使用encode_queries将这个查询转换为嵌入。接下来我们可以执行向量搜索以获得最相似的产品。

设置Milvus客户端

code block

code block

code block

code block

我们得到了结果。根据搜索结果，与我们查询最相似的产品是'Cloudz"The Big Bag" Travel & Sport Duffle Bag'，这在我们的产品标题目录中是准确的。

通过Milvus，你还可以执行其他复杂的向量搜索。例如，你可以在向量搜索的同时执行元数据过滤，以获得更好的搜索准确性。 此外，我们还可以执行混合搜索。这种搜索结合了BM25的稀疏向量和通常由句子变换器或OpenAI的深度学习模型产生的密集向量，以提供更准确的产品推荐。

BM25算法的进展

在其诞生之后，研究人员提出了几种BM25优化变体，以扩展其在复杂信息检索场景中的功能。

第一个是BM25F，代表带有字段的最佳匹配25。BM25F扩展了BM25算法，以处理具有结构化字段的文档，例如包含多个字段（如标题、正文、作者等）的文档。在BM25F中，文档的每个字段分别处理，并且为每个字段单独计算BM25分数。然后使用加权求和或其他聚合方法将这些分数组合起来，以产生文档的最终相关性分数。

第二个是BM25+或带有相关性反馈的最佳匹配25。在BM25+中，使用来自先前搜索结果或用户交互的反馈信息来调整文档的相关性分数。被用户积极评价或点击的文档将获得更高的相关性分数，而被负面评价的文档将获得较低的分数。

结论

BM25算法可以看作是对传统TF-IDF方法的改进，使其能够处理复杂的信息检索场景。在BM25中应用的重要改进包括术语频率饱和和文档长度归一化。我们可以使用BM25变量（如k和b）调整这两个因素的影响。 我们可以轻松地实现BM25算法，将文档和查询转换为Milvus中的稀疏向量。然后，这些稀疏向量可用于向量搜索，以根据特定查询找到最相关的文档。