理解神经网络中的正则化

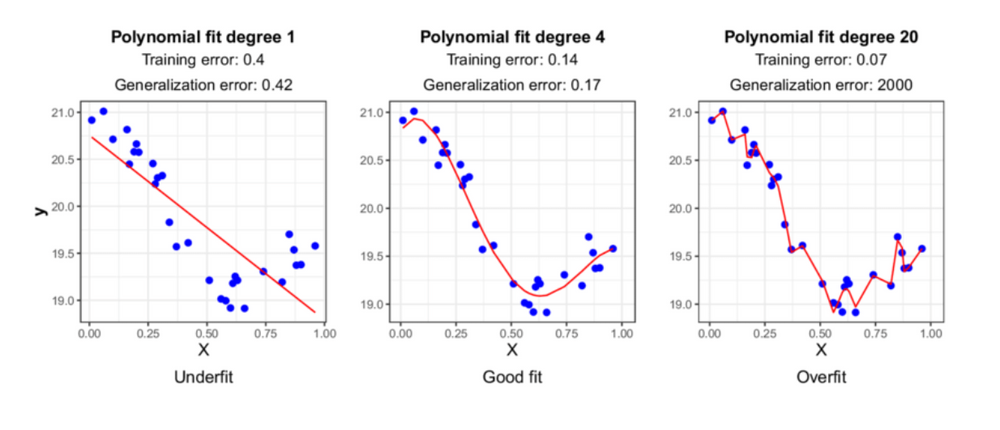
模型过拟合并正则化

为了让机器学习模型在现实世界的应用中有用，它应该能够将其预测推广到训练数据之外。这意味着它应该能够准确预测它以前未见过的新数据。

然而，有几个因素可能会阻止机器学习模型有效地推广其预测。最常见的原因之一是模型过拟合。当模型尝试过于努力地适应其训练数据的模式时，就会导致在未见过的数据上表现不佳。

作为一个类比，考虑一个学生，他逐字逐句地记忆教科书和练习考试，而不是理解背后的概念。这个学生可能在与他们的学习材料非常相似的测试上表现得非常好，因为他们可以在给出熟悉的问题时完美地背诵答案。然而，当面临新问题或被要求在不同的情境中应用他们的知识时，他们就会显著地挣扎。当模型过拟合训练数据时，也会发生同样的事情。

正则化是一种旨在防止机器学习模型在训练过程中过拟合的技术。在本文中，我们将讨论各种正则化技术。但在那之前，我们首先必须理解偏差和方差的概念。

偏差和方差以及它们与过拟合的关系

偏差和方差是机器学习模型训练中的两个重要概念。它们衡量了模型在训练过程中的不同方面的行为：

• 偏差：衡量模型预测的平均值与训练数据的实际值之间的差异。如果模型偏差较高，通常是因为它太简单，无法捕捉训练数据的模式。
• 方差：衡量如果我们使用不同的训练数据集，模型的预测会有多大变化。高方差表明模型对训练集的微小波动过于敏感，这可能导致过拟合。

偏差和方差的概念与欠拟合和过拟合的问题密切相关。

欠拟合发生在模型无法捕捉数据的模式时。换句话说，它具有高偏差和低方差，导致训练和测试数据表现不佳。解决欠拟合的方法是通过向神经网络架构添加更多层来增加模型的复杂性。

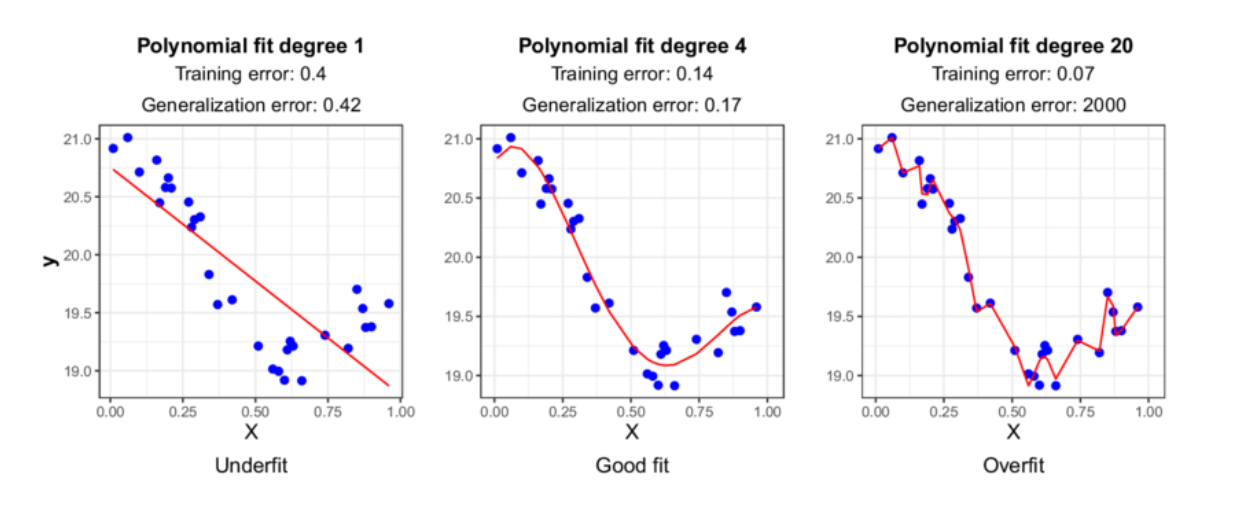Figure_1_Underfitting_vs_Good_fit_vs_Overfitting_f5a38c7828.png

图1：欠拟合 vs 良好拟合 vs 过拟合。

另一方面，当模型尝试过于努力地遵循训练数据的模式时，就会发生过度拟合，导致对未见过的数据泛化能力差。换句话说，它具有低偏差和高方差。我们需要应用正则化技术来避免过拟合，我们将在下一部分讨论。

根据上述偏差和方差的概念，理想的情况是拥有一个偏差和方差值都足够低的模型。然而，由于各种原因，如噪声数据、数据不足、计算资源等，这通常并不可行。因此，目标实际上是在偏差-方差权衡中找到最佳点，使模型在训练和测试数据上都能以合理的准确性表现。

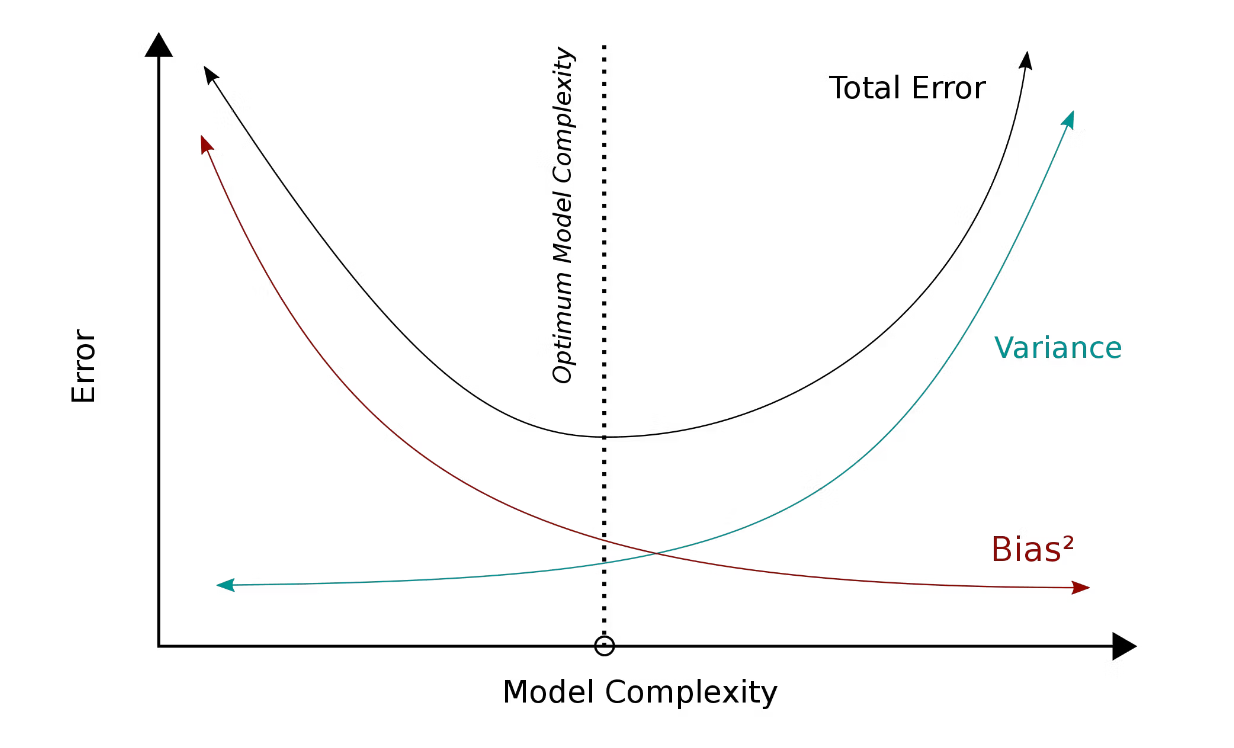Figure_2_Bias_and_variance_trade_off_1bf38cbdd3.png

图2：偏差和方差的权衡。

我们在下一部分讨论的正则化技术旨在降低模型的方差，使其能够在未见过的数据上很好地泛化。

不同类型的正则化技术

有几种正则化技术可用于改善模型对未见过数据的泛化。在本节中，我们将讨论最常应用的一些技术，包括 L1 和 L2 正则化、Elastic Net、早停、Dropout、批量归一化和数据增强。让我们从 L1 和 L2 正则化开始。

L1 和 L2 正则化

要理解 L1 和 L2 正则化的概念，让我们回顾一下在训练过程中如何优化神经网络的权重。

在每个 epoch 或训练步骤中，我们需要根据任务的目标计算模型的损失函数。如果是分类，我们通常使用二元或分类交叉熵，如果是回归问题，我们通常使用均方误差。

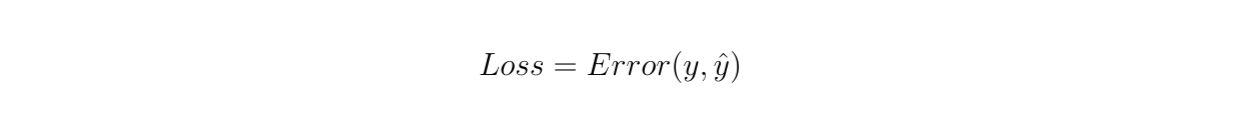Figure_3_Compute_the_loss_function_of_our_model_b2ccd89402.png

图3：计算模型的损失函数。

接下来，神经网络通过梯度下降算法进行优化过程。在这一步中，我们首先计算损失函数相对于权重的偏导数。然后，我们通过减去导数结果和预先定义的学习率（λ）的乘积来更新模型的权重。

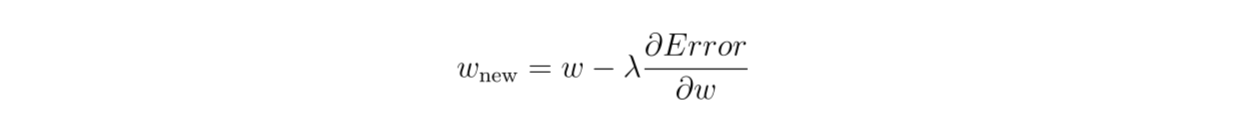Figure_4_Perform_gradient_descent_algorithm_f9f9d75bb4.png

图4：执行梯度下降算法。

L1 和 L2 正则化都通过在损失函数公式内添加一个惩罚项来工作。这个项惩罚大权重，并将它们推向零。可以想象，如果我们有一个神经网络，而且大多数权重接近或正好是零，那么我们最终将得到一个简单得多的神经网络。

过拟合的一个常见来源是模型对于训练数据来说过于复杂。通过将权重惩罚接近零，我们本质上降低了模型的复杂性，从而降低了方差。

L1 和 L2 正则化之间的唯一区别是损失函数计算中添加的惩罚项。让我们先从 L1 正则化开始。

L1 正则化

在 L1 正则化中，损失函数内的额外惩罚项将是模型中所有权重的总和与惩罚参数 α 的乘积。这个惩罚参数需要预先定义，它决定了正则化效果的大小。

如果我们计算这个额外惩罚项相对于模型权重的偏导数，我们最终会得到以下等式：

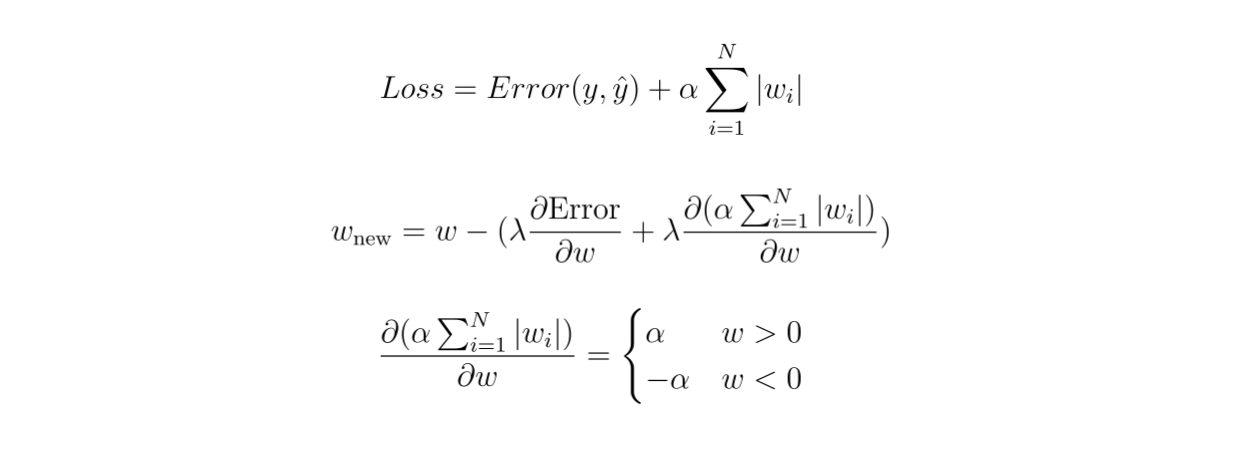Figure_5_Compute_the_partial_derivative_of_the_additional_penalty_term_in_L1_regularization_3127dd02ca.png

图5：计算 L1 正则化中额外惩罚项的偏导数。

如您所见，如果权重是正数，惩罚参数将减去权重，使其不那么正，更接近零。与此同时，如果权重是负数，惩罚参数将增加权重，使其不那么负，也更接近零。

这种正则化方法经常将模型中的大多数权重推向零，导致在训练过程中估计数据的模型复杂性降低。

L2 正则化

L2 正则化的惩罚项与 L1 略有不同。L2 正则化在惩罚项中实现了平方或 L2 范数，如下式所示：

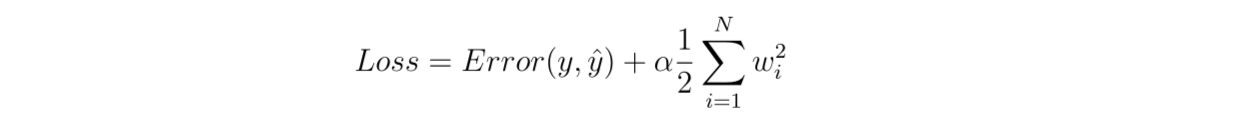Figure_6_Compute_the_partial_derivative_of_the_additional_penalty_term_in_L2_regularization_eaea2188ad.png

图6：计算 L2 正则化中额外惩罚项的偏导数。

如果我们计算损失函数相对于权重的偏导数，我们最终会得到以下等式：

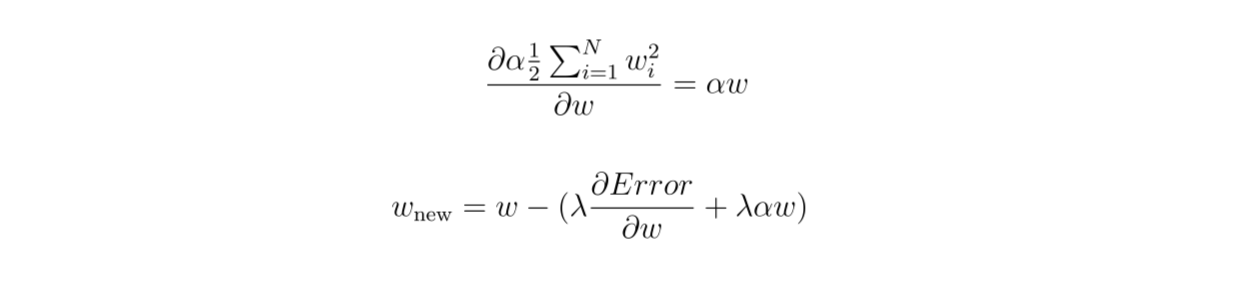Figure_7_Calculate_the_partial_derivative_of_the_loss_function_b827f8a8f0.png

图7：计算损失函数相对于权重的偏导数。

如您所见，在 L2 正则化中，权重的惩罚不仅仅由权重本身的符号决定，还由其大小决定。因此，权重不会像在 L1 正则化中那样积极地被推向零。然而，权重在这种正则化之后仍然有可能变为零。

Elastic Net

Elastic Net 是一种将 L1 和 L2 正则化合并为一个加权惩罚项并添加到损失函数内的方法。这意味着 L1 和 L2 惩罚参数的总和将达到一。

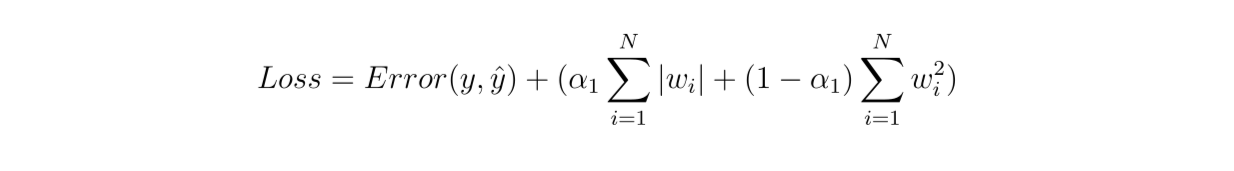Figure_8_Elastic_Net_c741c89cc4.png

图8：Elastic Net

Elastic Net 的主要目标是让我们能够获得 L1 和 L2 正则化的双重优势：它像 L1 一样有效地减少某些特征，但不至于积极地将权重推向零。另一方面，它也可以有效地减少不那么重要的特征的系数，正如 L2 正则化所做的。

现在让我们一次性实现 L1、L2 和 Elastic Net。由于 Elastic Net 是 L1 和 L2 的组合，我们将主要关注 Elastic Net 的实现，尽管您可以通过注释代码的某些部分来切换到 L1 或 L2。如果您想跟随操作，本文中的所有代码都在这个笔记本中可用。

首先，让我们导入库并初始化一个 3 层神经网络。

import os
import torch
from torch import nn
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from torchvision import transforms
from tqdm import tqdm
from torch.utils.data import Dataset

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

class MLP(nn.Module):

     def __init__(self):
         super().__init__()
         self.layers = nn.Sequential(
         nn.Flatten(),
         nn.Linear(28 * 28 * 1, 64),
         nn.ReLU(),
         nn.Linear(64, 32),
         nn.ReLU(),
         nn.Linear(32, 10)
         )

      def forward(self, x):
           return self.layers(x)

      def compute_l1_loss(self, w):
           return torch.abs(w).sum()

      def compute_l2_loss(self, w):
           return torch.square(w).sum()

我们在上面的模型架构中实现了 L1 和 L2 正则化的惩罚项计算。接下来，让我们定义 Elastic Net 的训练过程，并在 MNIST 手写数字数据集上训练模型。如果您想切换到仅使用 L1 或 L2，在笔记本或以下实现中提到的特定代码部分注释掉：

def train(model, dataset, epochs, lr):

  train_loader = torch.utils.data.DataLoader(dataset, batch_size=10, shuffle=True, num_workers=1)
  loss_function = nn.CrossEntropyLoss()
  optimizer = torch.optim.Adam(model.parameters(), lr=lr)

  for epoch in range(epochs):
    total_loss = 0

    for data in tqdm(train_loader):

        inputs, targets = data
        optimizer.zero_grad()
        outputs = model(inputs.to(device))
        loss = loss_function(outputs, targets.to(device))
        
        l1_weight = 0.4 #Or 1.0 for L1 regularization
        l2_weight = 0.6 #Or 1.0 for L2 regularization

        # Compute L1 and L2 loss component
        # Comment out L1 or L2 depending on regularization you use
        # If you use L1, comment out l2 and vice versa
        parameters = []
        for parameter in model.parameters():
            parameters.append(parameter.view(-1))
        l1 = l1_weight * model.compute_l1_loss(torch.cat(parameters))
        l2 = l2_weight * model.compute_l2_loss(torch.cat(parameters))

        # Add loss component
        # Comment out L1 or L2 depending on regularization you use
        # If you use L1, comment out l2 and vice versa
        loss += l1
        loss += l2
        total_loss += loss.item()

        loss.backward()
        optimizer.step()

    print(f'Epochs: {epoch + 1} | Loss: {total_loss / len(dataset): .3f}')

# train model on MNIST data
EPOCHS = 5
LEARNING_RATE = 1e-4
dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
model = MLP().to(device)
train(model, dataset, EPOCHS, LEARNING_RATE)

早停

过拟合发生是因为模型过于努力地遵循训练数据的模式。**当使用过于复杂的模型并在简单数据上训练时，这种情况尤其常见。因此，观察模型在训练期间对验证数据的表现是一种识别和缓解模型过拟合的方法。

在理想情况下，我们希望模型在每次训练迭代中对训练和验证数据的错误都减少。然而，如果训练数据的错误持续减少，而验证数据的错误开始增加，这显然是我们的模型过拟合训练数据的迹象。

解决这个问题的一种方法是仅训练我们的神经网络模型足够的迭代次数。然而，几乎不可能提前知道给定数据集的最佳训练迭代次数。我们可以将训练迭代次数设置为超参数，然后使用不同的迭代值训练模型，选择在验证数据上结果最佳的模型。然而，这种方法效率低下，因为它需要昂贵的计算资源，特别是当我们的模型庞大复杂，并且我们还有一个巨大的数据集时。

Figure_9_Early_stopping_strategy_8bfda98553.png

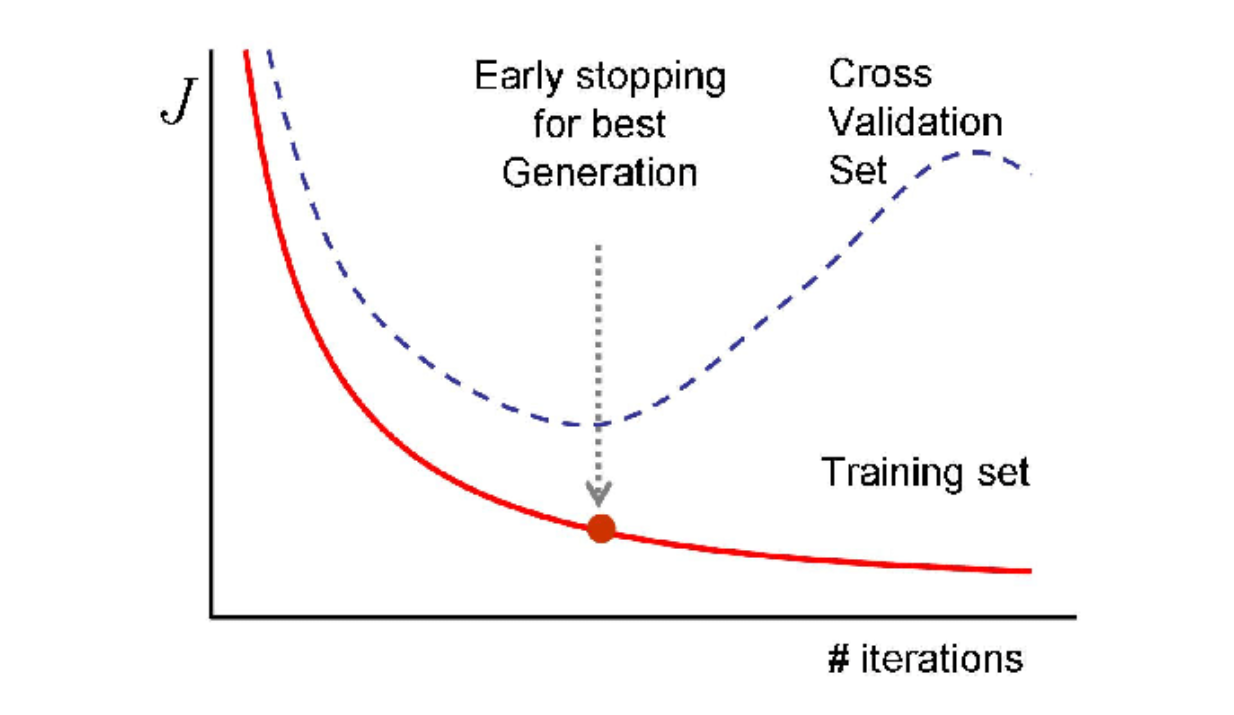
图9：早停策略。

早停是一种解决上述问题的正则化方法。其概念很简单：我们监控每次迭代中验证损失的值。一旦验证损失开始增加，我们立即停止训练过程。

在实践中，由于训练过程中的随机性，迭代中的验证损失高于前一次的情况是相当常见的。因此，我们通常在使用早停时实现一个容忍值。例如，如果容忍值设置为 2，当验证错误在两个连续的迭代中没有改善时，该方法将停止训练过程。

让我们用之前实现的相同模型和数据实现早停。我们将验证错误的容忍度设置为 2，这意味着如果验证错误在两个连续的 epoch 中没有改善，我们将停止训练。

def train_with_early_stopping(model, train_dataset, val_dataset, epochs, lr, patience):

  train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=10, shuffle=True, num_workers=1)
  val_loader = torch.utils.data.DataLoader(val_dataset, batch_size=10, shuffle=True, num_workers=1)

  loss_function = nn.CrossEntropyLoss()
  optimizer = torch.optim.Adam(model.parameters(), lr=lr)

  best_loss = 100000
  best_epoch = 0
  for epoch in range(epochs):

        for data in tqdm(train_loader):
        
              inputs, targets = data
              optimizer.zero_grad()
        
              outputs = model(inputs.to(device))
              loss = loss_function(outputs, targets.to(device))
        
              loss.backward()
              optimizer.step()
    
        with torch.no_grad():
              total_loss_val = 0
              for val_data in tqdm(val_loader):
        
                  inputs, targets = val_data
                  outputs = model(inputs.to(device))
        
                  loss = loss_function(outputs, targets.to(device))
                  total_loss_val += loss.item()
    
        avg_loss = total_loss_val / len(val_dataset)
        print(f'Epochs: {epoch + 1} | Val Loss: {avg_loss: .10f}')
    
        if avg_loss < best_loss:
            best_loss = avg_loss
            best_epoch = epoch
            torch.save(model.state_dict(), "best_model.pt")
    
        elif epoch - best_epoch > patience:
            print("Early stopped training at epoch %d" % epoch)
            break  # terminate the training loop

# train the model
PATIENCE = 2
EPOCHS = 1000
LEARNING_RATE = 1e-4
dataset = MNIST(os.getcwd(), download=True, transform=transforms.ToTensor())
train_set, val_set = torch.utils.data.random_split(dataset, [50000, 10000])
model = MLP().to(device)
train_with_early_stopping(model, train_set, val_set, EPOCHS, LEARNING_RATE, PATIENCE)

Droupout

本质上，Dropout 是一种常用于神经网络架构的正则化技术，通过在训练过程中随机丢弃一个或多个神经元来实现。这意味着在训练期间，被丢弃神经元的权重不会在反向传播过程中更新。

要实现 Dropout，我们首先需要为每一层定义一个丢弃概率。例如，假设我们在一层中设置了 50% 的丢弃概率。这意味着在训练期间，该层中的每个神经元都有 50% 的机会被丢弃。这个过程在每个训练批次中独立发生，这意味着同一迭代中的不同数据子集由于每层中随机丢弃的神经元将很可能具有不同的模型架构。

Figure_9_Architecture_of_a_neural_network_before_and_after_dropout_ee8c9e48d6.png

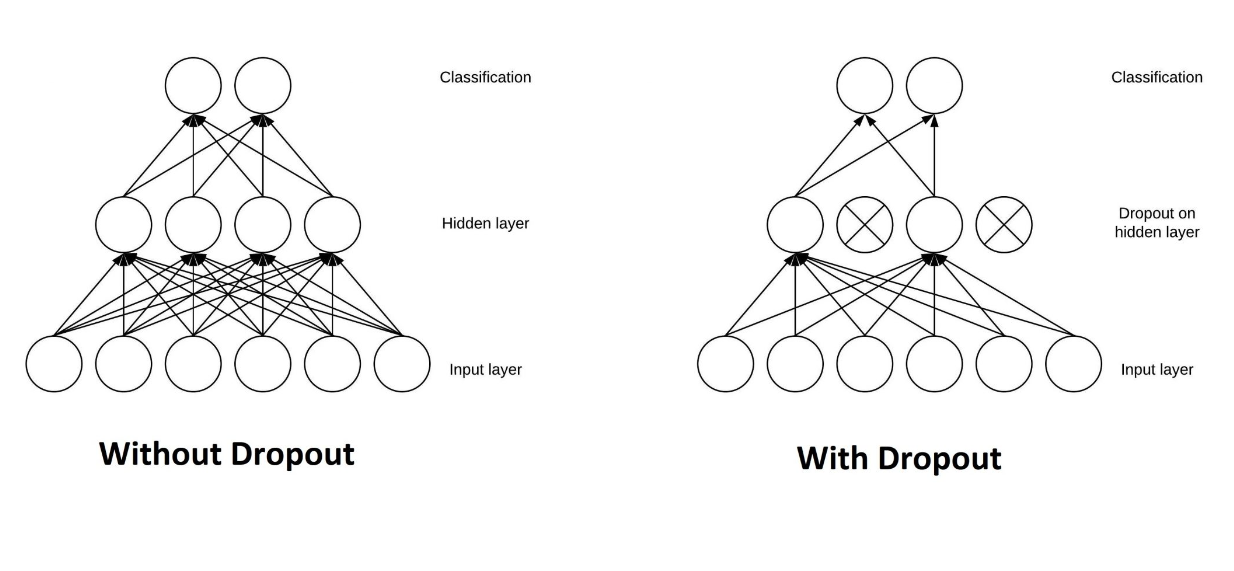
图10：Dropout 前后神经网络的架构。

这种正则化方法是相当破坏性的，但它已被证明在改善模型对未见过数据的泛化能力方面有效。如前一节所述，过拟合的一个原因是模型过于复杂。可以想象，如果我们在每一层随机丢弃神经元，我们最终将得到一个简单得多的模型。

此外，如果在训练期间随机丢弃神经元，其他神经元需要介入并进行必要的权重调整，以便能够正确预测训练数据。这反过来将使整体模型对特定层中神经元的特定权重的敏感性降低，从而导致具有更好泛化能力的模型。

需要注意的一件重要事情是，在推理期间我们不能丢弃任何层中的神经元。因此，在 PyTorch 中，特定层在训练期间的激活输出已按 1/（1-p）缩放，其中 p 是该层中神经元被丢弃的概率。在推理期间，我们只需计算一个恒等函数。

在下面的代码实现中，我们将创建一个具有 50% 丢弃概率的 Dropout 层的模型。接下来，我们可以像前面演示的那样正常训练它。

class MLP_Dropout(nn.Module):

  def __init__(self):
       super().__init__()
       self.layers = nn.Sequential(
         nn.Flatten(),
         nn.Linear(28 * 28 * 1, 64),
         nn.Dropout(p=0.5),
         nn.ReLU(),
         nn.Linear(64, 32),
         nn.Dropout(p=0.5),
         nn.ReLU(),
         nn.Linear(32, 10)
       )

  def forward(self, x):
       return self.layers(x)

model_dropout = MLP_Dropout().to(device)
EPOCHS = 5
train_with_early_stopping(model_dropout, train_set, val_set, EPOCHS, LEARNING_RATE, PATIENCE)

批量归一化

批量归一化是一种通过每个训练批次的均值和标准差来规范化层输入的技术。

那么问题来了：为什么批量归一化作为一种正则化技术有效？

正如您可能已经知道的那样，神经网络对学习算法的设置非常敏感，例如学习率、批量大小、权重初始化、优化算法等。在训练过程中，每层的权重被更新，以准确地将输入数据映射到相应的真实值，给定来自前一层的输出。

问题在于，大多数训练数据具有不同的分布，这可能导致学习算法追逐一个移动的目标。一个层的权重可能会被大幅更新，以优化输入到其标签的映射，给定来自前一层的激活输出。因此，算法需要更多的迭代来学习。批量归一化通过将输入规范化为其均值和标准差来帮助稳定和加速学习过程。

除了稳定和加速学习过程外，输入规范化还引入了一些随机性。这种方法通常每个批次执行一次，因此输入在每个批次中都有自己的均值和标准差。因此，网络在每个批次中看到不同的输入，防止其记忆训练数据并避免过拟合。

以下是一个如何在 PyTorch 中实现批量归一化的示例。在实现批量归一化的模型后，您可以立即使用与之前相同的方法进行训练。

class MLP_BN(nn.Module):

  def __init__(self):
       super().__init__()
       self.layers = nn.Sequential(
         nn.Flatten(),
         nn.Linear(28 * 28 * 1, 64),
         nn.BatchNorm1d(64),
         nn.ReLU(),
         nn.Linear(64, 32),
         nn.BatchNorm1d(32),
         nn.ReLU(),
         nn.Linear(32, 10)
       )

  def forward(self, x):
       return self.layers(x)

model_bn = MLP_BN().to(device)
EPOCHS = 5
train_with_early_stopping(model_bn, train_set, val_set, EPOCHS, LEARNING_RATE, PATIENCE)

数据增强

数据增强有助于防止过拟合，原因显而易见：它有助于增加训练数据的大小。如前一节所述，当在有限的训练数据上训练过于复杂的模型时，可能会发生过拟合。如果我们能够设法增加训练数据，我们模型的泛化误差将会减少。

我们可以实施几种常见的数据增强方法来增加数据。如果我们处理的是图像，我们可以执行图像旋转、翻转、缩放、裁剪或移动。与此同时，如果我们处理的是文本数据，我们可以将单词替换为它们的同义词或使用生成性 AI 生成语义相似的文本。

以下是对 MNIST 数据进行几种图像数据增强的示例：

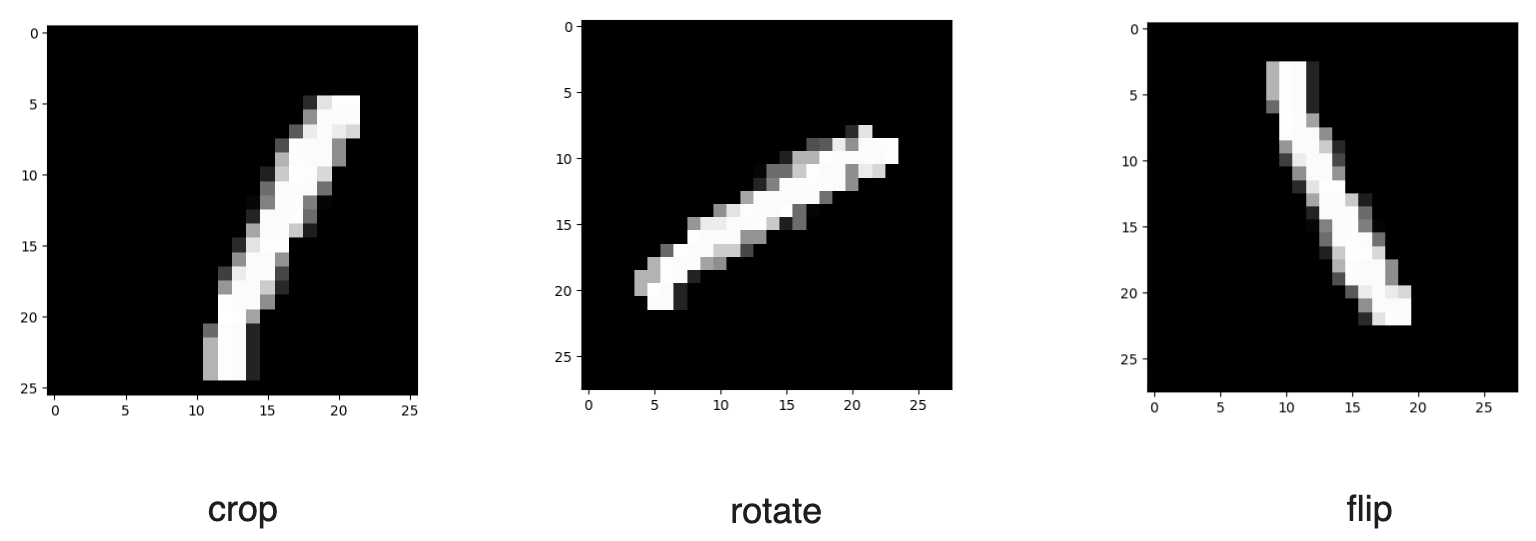Figure_10_Several_examples_of_image_augmentation_of_MNIST_handwritten_digits_dataset_8751176f5b.png

图11：MNIST 手写数字数据集的几种图像增强示例。

我们可以使用 torchvision 库中的 transforms.Compose() 方法在 PyTorch 中执行图像数据增强。在这个方法中，您可以指定您想要实现的图像数据增强方法。

在下面的代码中，我们将实现三种图像增强：裁剪、翻转和旋转。如果您想了解其他图像增强方法，请查看 PyTorch 的这个资源。

transform_train = transforms.Compose([
              transforms.ToTensor(),
              transforms.RandomCrop(28, padding=4),
              transforms.RandomVerticalFlip(),
              transforms.RandomRotation(50)])

model = MLP().to(device)
EPOCHS = 5
LEARNING_RATE = 1e-4
dataset = MNIST(os.getcwd(), download=True, transform=transform_train)
train(model, dataset, EPOCHS, LEARNING_RATE)

结论

过拟合是机器学习模型过于努力地遵循训练数据的模式，导致在未见过的数据上表现不佳的一种情况。正则化是神经网络训练过程中常用的一种技术，用于防止过拟合。

实践中几种常用的正则化包括 L1 和 L2 正则化、Elastic Net、早停、Dropout、批量归一化和数据增强。尽管这些技术对正则化机器学习模型的方法不同，但它们的目标是相同的：减少模型的方差并增加偏差。这样，模型可以在偏差-方差的权衡中实现最佳点。

注：本文为AI翻译，查看原文